El Desafío del Empaque en Contenedores: Optimizando Espacios en contenedores con Ingenio
Algoritmos y Ejemplos en Python

¿Qué es el Problema de Embalaje en Contenedores?
El bin packing problem es un problema NP-difícil, lo que significa que no se conoce un algoritmo eficiente para resolverlo de forma óptima en casos grandes. El objetivo es asignar ítems de diferentes tamaños a contenedores de capacidad fija usando el menor número posible de contenedores.
Entrada y Salida
- Entrada:
- Lista de ítems con tamaños (e.g., pesos o dimensiones).
- Capacidad máxima de cada contenedor.
- Salida: Asignación de ítems a contenedores, minimizando el número total de contenedores.
Existen variantes como 1D (una dimensión, e.g., peso) y 2D (ancho y alto), comunes en logística y empaquetado.
Algoritmos para Resolver el Problema
A continuación, exploramos cuatro algoritmos clave, sus estrategias y cómo implementarlos en Python.
1. First Fit Decreasing (FFD)
Este algoritmo ordena los ítems de mayor a menor y los coloca en el primer contenedor con espacio suficiente. Es simple y efectivo, con una complejidad de O(n log n) debido a la ordenación.
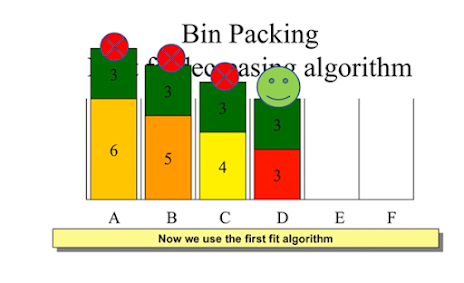
Ilustración del algoritmo First Fit Decreasing, mostrando ítems ordenados y colocados en contenedores (Fuente: ResearchGate).
Algoritmo First Fit Decreasing (FFD) en python
def first_fit_decreasing(items, bin_capacity):
# Ordenar ítems en orden descendente
sorted_items = sorted(items, reverse=True)
bins = [[]] # Lista inicial con un contenedor vacío
for item in sorted_items:
placed = False
# Buscar el primer contenedor con espacio suficiente
for bin in bins:
if item <= bin_capacity - sum(bin):
bin.append(item)
placed = True
break
# Si no cabe, crear un nuevo contenedor
if not placed:
bins.append([item])
return len(bins), bins
# Ejemplo
items = [4, 8, 1, 2, 5, 3]
bin_capacity = 10
num_bins, bins = first_fit_decreasing(items, bin_capacity)
print(f"Número de contenedores: {num_bins}")
print(f"Ítems en contenedores: {bins}")
2. Best Fit
Este algoritmo coloca cada ítem en el contenedor con la menor capacidad restante que pueda alojarlo, minimizando el espacio desperdiciado. Complejidad: O(n²).
Algoritmo Best Fit en python
def best_fit(items, bin_capacity):
bins = []
for item in items:
placed = False
min_remaining_capacity = bin_capacity
best_bin = None
# Buscar el contenedor con la menor capacidad restante
for bin in bins:
remaining_capacity = bin_capacity - sum(bin)
if item <= remaining_capacity and remaining_capacity < min_remaining_capacity:
best_bin = bin
min_remaining_capacity = remaining_capacity
placed = True
# Si no cabe, crear un nuevo contenedor
if not placed:
best_bin = []
bins.append(best_bin)
best_bin.append(item)
bins = [bin for bin in bins if bin] # Eliminar contenedores vacíos
return len(bins), bins
# Ejemplo
items = [4, 8, 1, 2, 5, 3]
bin_capacity = 10
num_bins, bins = best_fit(items, bin_capacity)
print(f"Número de contenedores: {num_bins}")
print(f"Ítems en contenedores: {bins}")
3. Next Fit
Coloca cada ítem en el último contenedor abierto. Si no cabe, crea un nuevo contenedor. Es rápido (O(n)), pero menos eficiente en espacio.
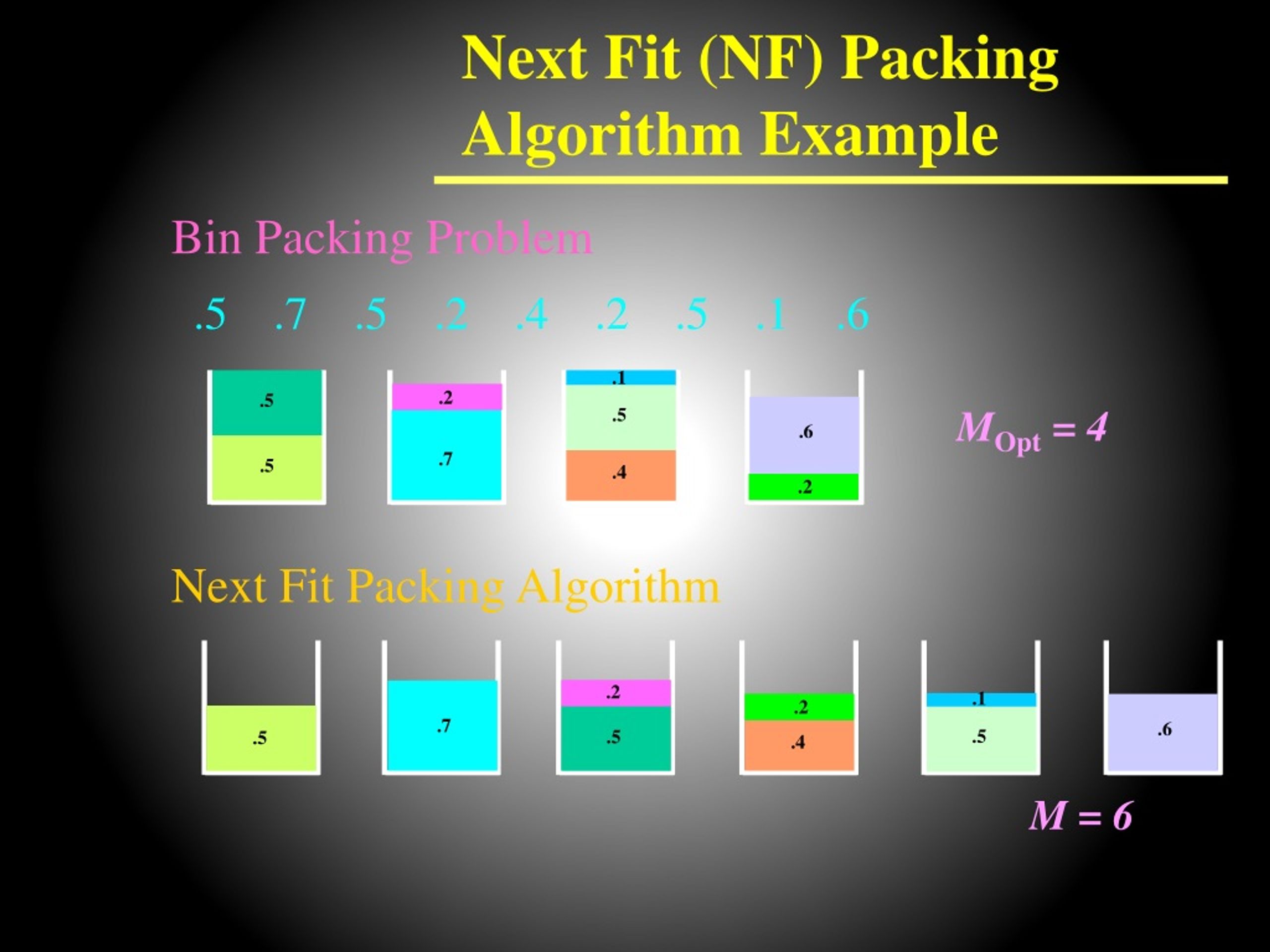
Algoritmo Next Fit en python
def next_fit(items, bin_capacity):
bins = [[]]
for item in items:
current_bin = bins[-1]
if item <= bin_capacity - sum(current_bin):
current_bin.append(item)
else:
bins.append([item])
return len(bins), bins
# Ejemplo
items = [4, 8, 1, 2, 5, 3]
bin_capacity = 10
num_bins, bins = next_fit(items, bin_capacity)
print(f"Número de contenedores: {num_bins}")
print(f"Ítems en contenedores: {bins}")
4. Algoritmos Genéticos
Estos algoritmos metaheurísticos, inspirados en la evolución natural, generan soluciones aproximadas mediante selección, cruce y mutación. Son ideales para problemas complejos, pero requieren ajuste de parámetros.

Algoritmo genético en python
import random
def evaluate(individual, items, bin_capacity):
bins = [[]]
current_bin_index = 0
current_bin_capacity = bin_capacity
for item, bin_bit in zip(items, individual):
if item <= current_bin_capacity:
bins[current_bin_index].append(item)
current_bin_capacity -= item
else:
current_bin_index += 1
current_bin_capacity = bin_capacity
bins.append([item])
current_bin_capacity -= item
return len(bins), bins
def crossover(parent1, parent2):
crossover_point = random.randint(1, len(parent1) - 1)
return parent1[:crossover_point] + parent2[crossover_point:]
def mutate(individual, mutation_rate):
mutated_individual = individual[:]
for i in range(len(mutated_individual)):
if random.random() < mutation_rate:
mutated_individual[i] = 1 - mutated_individual[i]
return mutated_individual
def genetic_algorithm(items, bin_capacity, population_size, generations, mutation_rate):
population = [random.choices([0, 1], k=len(items)) for _ in range(population_size)]
for _ in range(generations):
fitness_scores = [evaluate(individual, items, bin_capacity)[0] for individual in population]
parents = random.choices(population, weights=[1/score for score in fitness_scores], k=population_size)
offspring = []
while len(offspring) < population_size:
parent1, parent2 = random.sample(parents, 2)
child = crossover(parent1, parent2)
child = mutate(child, mutation_rate)
offspring.append(child)
population = offspring
best_individual, bins = min([(evaluate(individual, items, bin_capacity)[0], evaluate(individual, items, bin_capacity)[1]) for individual in population], key=lambda x: x[0])
utilized_bins = [bin for bin in bins if bin]
for i, bin_items in enumerate(utilized_bins):
print(f"Contenedor {i + 1}: {bin_items}")
return len(utilized_bins)
# Ejemplo
items = [4, 8, 1, 2, 5, 3]
bin_capacity = 10
population_size = 100
generations = 50
mutation_rate = 0.01
num_bins = genetic_algorithm(items, bin_capacity, population_size, generations, mutation_rate)
print(f"Número de contenedores: {num_bins}")
population_size y generations según el tamaño del problema para mejores resultados.
Comparación de Algoritmos
La elección del algoritmo depende del caso de uso. A continuación, una tabla comparativa:
| Algoritmo | Complejidad | Ventajas | Desventajas |
|---|---|---|---|
| First Fit Decreasing | O(n log n) | Rápido, fácil de implementar | No siempre óptimo |
| Best Fit | O(n²) | Minimiza espacio desperdiciado | Más lento |
| Next Fit | O(n) | Muy rápido, ideal para tiempo real | Peor uso del espacio |
| Algoritmos Genéticos | Variable (depende de parámetros) | Bueno para problemas complejos | Requiere ajuste, no garantiza óptimo |
Ejemplo Práctico: Resultados
Para los ítems [4, 8, 1, 2, 5, 3] con capacidad de contenedor 10, los algoritmos producen:
- FFD: 3 contenedores ([8], [5, 4], [3, 2, 1])
- Best Fit: 3 contenedores ([8, 2], [5, 4], [3, 1])
- Next Fit: 4 contenedores ([4], [8], [1, 2, 5], [3])
- Genéticos: Variable, pero tiende a 3 contenedores.
Conclusión
El problema de embalaje en contenedores es un desafío fascinante con aplicaciones en logística, computación y más. Los algoritmos como First Fit Decreasing, Best Fit, Next Fit y Genéticos ofrecen soluciones prácticas, cada uno con fortalezas específicas. ¡Prueba estos códigos en Python y optimiza tus propios problemas de empaquetado!
¿Tienes un caso real para aplicar estos algoritmos? ¡Déjanos un comentario y comparte tus resultados! 👇
¡Únete a la Comunidad!
🔔 Suscríbete para más contenido sobre algoritmos y Python.
📢 Comparte este artículo con tus colegas en LinkedIn.



