¡Optimización de Portafolios de Productos: El arte de maximizar el rendimiento!
Fuente: Hamish Thorburn
La optimización de portafolios de productos es clave para maximizar el rendimiento empresarial en industrias como retail, manufactura o tecnología. En este artículo, combinamos K-means clustering para agrupar productos similares y programación lineal con PuLP para construir portafolios óptimos, respetando restricciones como volumen, capacidad, precio y lead time. ¡Acompáñanos en este recorrido técnico!
El Problema de Optimización de Portafolios
Imagina que gestionas una empresa con múltiples productos, cada uno con características como volumen, precio, costo, lead time (tiempo de entrega) y calidad. El objetivo es construir portafolios de productos que maximicen el rendimiento total, cumpliendo restricciones como:
- Volumen mínimo por portafolio.
- Capacidad máxima por portafolio.
- Presupuesto o precio máximo.
- Lead time máximo permitido.
Nota: El clustering reduce la complejidad al agrupar productos similares, facilitando la optimización.
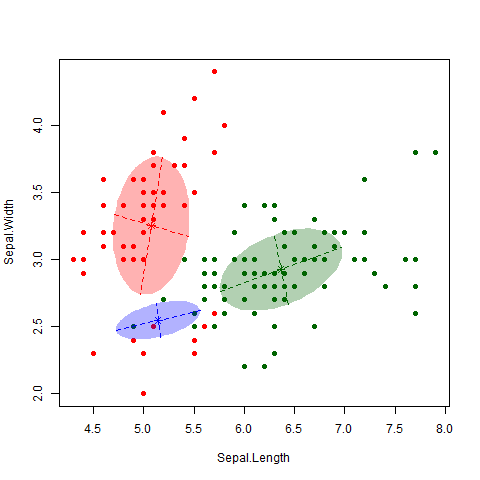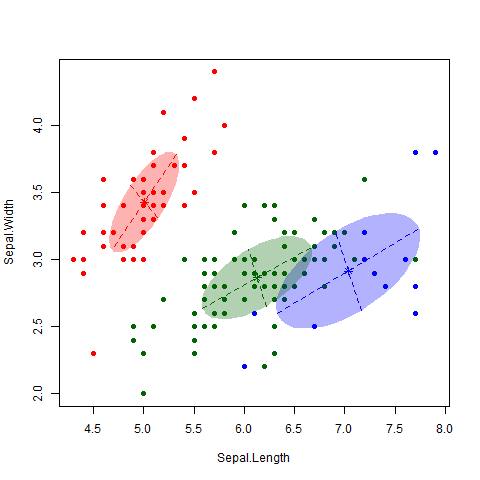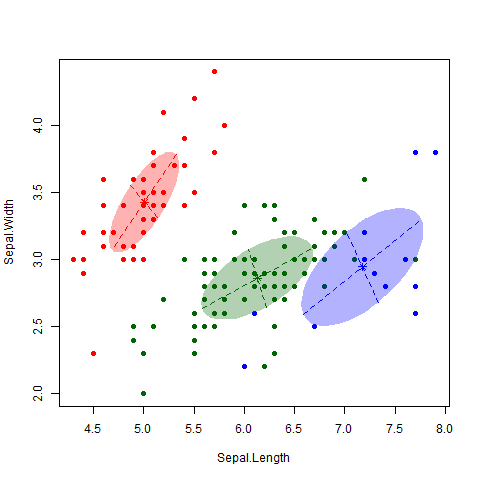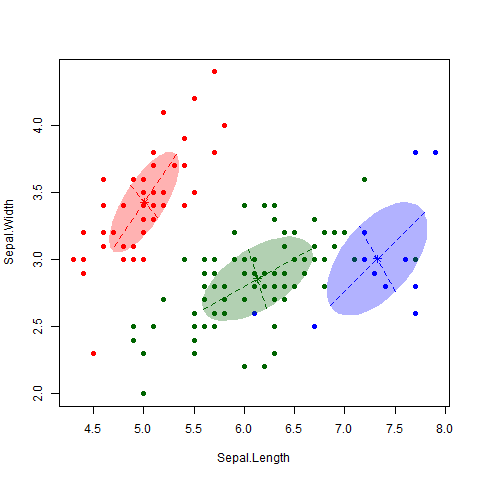
Agrupamiento con K-means
Usamos K-means para agrupar productos según sus características (volumen, precio, costo, lead time, calidad). Esto organiza los productos en \( k \) clusters, donde cada cluster representa un grupo de productos similares.
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
# Datos ficticios de productos
data = {
'Producto': ['A', 'B', 'C', 'D', 'E'],
'Volumen': [150, 100, 200, 120, 180],
'Precio': [50, 40, 60, 45, 55],
'Costo': [30, 25, 35, 28, 32],
'LeadTime': [5, 4, 6, 4, 5],
'Calidad': [0.8, 0.9, 0.7, 0.85, 0.9]
}
df = pd.DataFrame(data)
# Normalizar datos
X = df[['Volumen', 'Precio', 'Costo', 'LeadTime', 'Calidad']]
X_normalized = (X - X.mean()) / X.std()
# K-means (2 clusters)
kmeans = KMeans(n_clusters=2, random_state=42)
df['Cluster'] = kmeans.fit_predict(X_normalized)| Cluster | Productos |
|---|---|
| Cluster 0 | B, D |
| Cluster 1 | E |
Tip: Normaliza las características antes de aplicar K-means para evitar que variables con rangos grandes dominen el clustering.
Modelo de Programación Lineal
Función Objetivo
Restricciones
\[ \sum_{i \in \text{cluster } j} v_i \cdot w_i \leq 300 \quad \forall j \]
\[ 0 \leq w_i \leq 1 \quad \forall i \]
Implementación con PuLP
from pulp import *
# Problema
prob = LpProblem("Optimizacion_Portafolios", LpMaximize)
# Variables
products = df['Producto'].tolist()
weights = LpVariable.dicts("w", products, lowBound=0, upBound=1)
# Rendimientos
df['Rendimiento'] = df['Precio'] - df['Costo']
rendimientos = dict(zip(df['Producto'], df['Rendimiento']))
volumenes = dict(zip(df['Producto'], df['Volumen']))
# Objetivo
prob += lpSum([rendimientos[i] * weights[i] for i in products])
# Restricciones por cluster
clusters = df.groupby('Cluster')['Producto'].apply(list).to_dict()
for j in clusters:
prob += lpSum([volumenes[i] * weights[i] for i in clusters[j]]) >= 100
prob += lpSum([volumenes[i] * weights[i] for i in clusters[j]]) <= 300
# Resolver
prob.solve()
# Resultados
print("Estado:", LpStatus[prob.status])
for v in prob.variables():
if v.varValue > 0:
print(f"{v.name} = {v.varValue:.3f}")
print(f"Rendimiento Total = {value(prob.objective):.1f}")Resultados Óptimos
| Portafolio | Productos | Rendimiento | Volumen |
|---|---|---|---|
| Portafolio 1 | B, D | 200 | 220 |
| Portafolio 2 | E | 140 | 180 |
¡Portafolios óptimos generados con éxito!
¡Sigueme para más contenido!
LinkedInReferencias
[1] Scikit-learn: K-means Clustering – scikit-learn.org
[2] PuLP Documentation – coin-or.github.io/pulp

